This blog post was originally published at NVIDIA's website. It is reprinted here with the permission of NVIDIA.
The CUDA Fortran compiler from PGI now supports programming Tensor Cores with NVIDIA’s Volta V100 and Turing GPUs. This enables scientific programmers using Fortran to take advantage of FP16 matrix operations accelerated by Tensor Cores. Let’s take a look at how Fortran supports Tensor Cores.
Tensor Cores
Tensor Cores offer substantial performance gains over typical CUDA GPU core programming on Tesla V100 GPUs for certain classes of matrix operations running at FP16 (half-precision), as figure 1 shows.
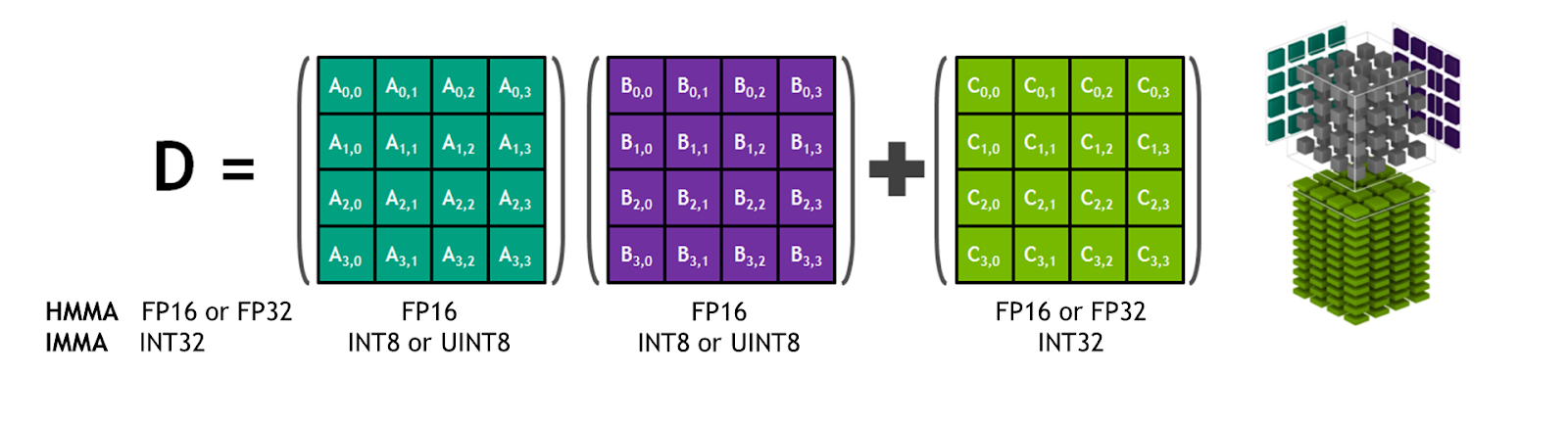
Figure 1. Tensor Cores accelerate certain classes of FP16 operations, enabling faster mixed-precision calculations while maintaining overall precision.
Those operations include matrix multiply of two forms. The first, simpler form:
Fortran: C = Matmul(A, B), where:
- A is a 2 dimensional array dimensioned A(m,k)
- B is a 2 dimensional array dimensioned B(k,n)
- C is a 2 dimensional array dimensioned C(m,n)
C(i,j) = sum(a(i,:) * b(:,j)), for i=1,m, j=1,n
A more general form which Tensor Cores support in hardware, is:
Fortran: D = C + Matmul(A, B), where:
- A, B, C are defined as above.
- D is a 2 dimensional array dimensioned D(m,n), similar to C.
The V100 hardware supports A and B as 16-bit floating point (real*2) data. C and D may be either 16-bit or 32-bit (real*4) data. Using 32-bit accumulation is usually advantageous since the only performance penalty comes from doubling the transfer and storage size. However, some 16-bit accumulation is found in practice. All combinations of 16 and 32-bit data types on C and D are supported by the hardware.
The Tensor Core unit itself supports 3 combinations of sizes for m, n, and k. The CUDA naming practice is to run the sizes together, so we will refer to them here as m16n16k16, m8n32k16, and m32n8k16. Note that k, the inner dot-product dimension, is always 16. For GPU memory arrays of different dimensions than these, it is the programmer’s responsibility to add padding and blocking.
C and D, of dimension m x n, always contain 256 elements. A and B may contain 128, 256, or 512 elements. These elements are divided among the threads in a warp. A key concept in programming Tensor Cores is that the storage and work carried out by each CUDA thread remains opaque. The threads in a warp cooperate to carry out the matrix multiplication. You should view the operation as a black box in which the answer shows up some small number of cycles after initiation. Every thread in the warp must take part in the operation for the results to be correct.
Tensor Core programming is a change to the traditional CUDA programming model, extending some of the ideas from cooperative groups and intra-warp shuffle operations. Data and operations on that data is considered “warp-level”, and not “CUDA thread-level”. PGI makes that distinction clear when choosing names of derived types and functions.
In CUDA C/C++, you can access and update the elements of the warp-level data structures with each thread. However, this is only possible for elemental operations such as scaling, offsetting, or setting/clearing the individual values. The mapping from a thread’s data to its position in the subMatrix is not visible or under programmer control. CUDA C/C++ declares a struct type __half, which contains an unsigned short, and a struct __half2, which contains two unsigned shorts, along with a large set of operations allowed on those types.
PGI Fortran Implementation
PGI 2019 implements a CUDA Fortran device module named WMMA (Warp-Matrix-Multiply-Add). You add the line use wmma in the declaration section of your device subroutines and functions to enable Tensor Core functionality.
This corresponds to the name of the CUDA C/C++ namespace, which looks like this in CUDA C++:
wmma::fragment<wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> c_frag;
Data Declaration
The Fortran declaration most synonymous with the C++ declaration shown above consists of parameterized derived types. In other words, the c_frag above might be declared this way:
type(fragment(wmmatype=acc, m=WMMA_M, n=WMMA_N, k=WMMA_K, kind=4)) :: c_frag
However, we’ve chosen to avoid that route. The PGI Fortran implementation stores the derived type parameters within the derived type, since derived type parameter enquiry must be supported by the language implementation. For example, print *,c_frag%m must work. Storing all of these parameters takes considerable register space which can adversely affect performance.
Instead, the WMMA module defines derived types which look like this:
type(subMatrixC_m16n16k16_Real4) :: c_frag
PGI recommends developers use the macros provided in the included example programs. Using macro pre-processing gives flexibility to use either parameterized derived type declarations or specific types in the future without affecting user code. Here is the declaration we currently use before macro pre-processing:
WMMASubMatrix(WMMAMatrixC, 16, 16, 16, Real, WMMAKind4) :: c_frag
Performance reasons dictate the underlying operations be called quickly without any runtime parameter inquiry overhead in both CUDA C++ and CUDA Fortran. Using C++ templates and these specific Fortran types allows for that.
The A and B subMatrix types must be distinct. Also, they must be defined as part of their declaration to be stored internally as either column major or row major. Our implementation today only supports real(2) data. WMMAColMajor and WMMARowMajor are defined in the WMMA module, yielding macro declarations which look like this:
WMMASubMatrix(WMMAMatrixA, 16, 16, 16, Real, WMMAColMajor) :: sa
WMMASubMatrix(WMMAMatrixB, 16, 16, 16, Real, WMMARowMajor) :: sb
Declaring B to be row major and using it in a Matmul operation is equivalent to this Fortran statement:
C = Matmul(A, Transpose(B))
Similarly, declaring A to be row major is equivalent to this:
C = Matmul(Transpose(A), B)
The C subMatrix is not declared with storage order but can be loaded and stored to memory in either order. For instance, storing the C result, computed in column major order, but stored in row major order, is equivalent to this:
C = Transpose(Matmul(A,B))
Users of the BLAS dgemm and other *gemm routines will recognize these transpose capabilities.
We use a 16-bit data type for both the larger matrices stored in CUDA global memory and for operating on the individual elements of the subMatrices. These will be real(2) in a future PGI release. Until then, we have created type macros which developers can use to get started with Tensor Cores. This is a straightforward translation; the simplest use case for the entire declaration section looks like this:
use wmma
CUFReal2, device :: a(m,k)
CUFReal2, device :: b(k,n)
real(4), device :: c(m,n)
WMMASubMatrix(WMMAMatrixA, 16, 16, 16, Real, WMMAColMajor) :: sa
WMMASubMatrix(WMMAMatrixB, 16, 16, 16, Real, WMMAColMajor) :: sb
WMMASubMatrix(WMMAMatrixC, 16, 16, 16, Real, WMMAKind4) :: sc
Basic WMMA Operations
Using the Tensor Cores at the most basic level means loading the input subMatrices from global memory, computing C = Matmul(A,B), and storing the result back to memory. The simplest use of the declarations above looks like this in Fortran:
call wmmaLoadMatrix(sa, a(1,1), m)
call wmmaLoadMatrix(sb, b(1,1), k)
call wmmaMatmul(sc, sa, sb)
call wmmaStoreMatrix(c(1,1), sc, m)
Each of these subroutines begin with a “wmma” prefix since they require every thread of the warp to make the call. The threads in each warp will cooperate to do the work.
The wmmaLoadMatrix subroutine takes as arguments the derived type to fill, the address of the global or shared memory upper left corner, and the stride between columns. The stride is required and corresponds to the lda, ldb, and ldc arguments in *gemm BLAS calls.
The wmmaMatmul subroutine can take 3 or 4 arguments. These uses are the most typical:
call wmmaMatmul(sc, sa, sb)
call wmmaMatmul(sc, sa, sb, sc)
call wmmaMatmul(sd, sa, sb, sc)
As mentioned above, A and B are always real(2), but can be any combination of column major or row major ordered. C and D can be any combination of real(2) and real(4).
For stores, wmmaStoreMatrix corresponds to wmmaLoadMatrix. The upper left corner in global or shared memory is the first argument. Then the type, then the stride. The A and B subMatrix types cannot be stored, only C. A fourth optional argument specifies the layout when the store occurs, either column major or row major. Column major is the default if neither is specified.
Advanced WMMA Operations
We’ve added some additional warp-level functionality and expect to work with our early adopters to fill in the gaps. The problems we expect developers to encounter include how to detect numeric issues and how to potentially fix them up within device kernels.
Treating the derived type subMatrices as just 2D numeric arrays through overloaded functions can solve some of these problems. Here are some things we’ve added.
Logical operations:
You can declare, or even generate without declaring, logical, kind=1, WMMA subMatrixC types. This allows logical operations between two WMMAMatrixC types, or between one C type and a scalar. These logical results can then be passed, in turn, to Fortran intrinsic functions like Merge(), and reductions like Any(), All(), and Count(). An example use might look like this:
WMMASubMatrix(WMMAMatrixC, 16, 16, 16, Real, WMMAKind4) :: sd
…
call wmmaMatmul(sd, sa, sb, sc)
if (wmmaAll(sd .lt. 64.0)) then
. . .
npos = wmmaCount(sd .ge. 0.0)
. . .
call wmmaMerge(sc, -99.0, sd, mask=sd.eq.sc)
If you prefer to use the standard Fortran intrinsic names, you can overload them on the use statement like this:
use wmma, any => wmmaAny, all => wmmaAll
It’s important to remember that in our naming convention, functions and subroutines that start with “wmma” imply the work is shared amongst the threads in a warp.
Merge()is a subroutine, while count(), any(), and all() are functions. In general, subprograms which natively return less than a 64-bit scalar work fine as device functions. It’s preferable to make array-valued subprograms and others returning large derived types subroutines for performance reasons. The returned value, or intent(out) array, or object is typically the first argument to such a routine.
Assignment
Initializing a subMatrix to zero is a basic operation:
sc = 0.0
You can also assign one subMatrixC type to another:
sc = sd
Operations on the Underlying WMMA Data
The WMMA module uses a naming convention in which the data held within the derived types is called x. The size of that data and how it maps to the original matrix locations may be subject to change. Operations on that data should be elemental and applied uniformly by all threads in the warp. Usage like that shown in the following code snippet should always be safe:
WMMASubMatrix(WMMAMatrixC, 16, 16, 16, Real, WMMAKind4) :: sd
real(4), device :: xoff, xtol
…
do klp = 1, maxtimes
if (wmmaAny(sd .gt. xtol)) then
do i = 1, size(sd%x)
sd%x(i) = sd%x(i) – xoff
end do
end if
end do
For the equivalent functionality using the current implementation when kind=2, declare the local scalars using the macro:
WMMASubMatrix(WMMAMatrixC, 16, 16, 16, Real, WMMAKind2) :: sd
CUFReal2 :: xoff, xtol, xtmp … xoff = CUFreal(10, kind=2)
…
do klp = 1, maxtimes
if (wmmaAny(sd .gt. xtol)) then
do i = 1, size(sd%x)
xtmp = sd%x(i)
sd%x(i) = xtmp – xoff
end do
end if
end do
Note that the compiler defines a function named CUFreal() to perform type conversions. Three specific cases are currently implemented:
- real2 = CUFReal(int4, kind=2)
- real2 = CUFReal(real4, kind=2)
- real4 = CUFReal(real2, kind=4)
We expect this function to change to the Fortran intrinsic real() when we add real(2) support to CUDA Fortran in an upcoming release. The macro will then be redefined to maintain backward compatibility. Equivalent in line operations on real(2) data will then be supported as well.
The most advanced users will see best performance when operating on the 16-bit data two at a time. We have an experimental module, named vector_types, which we provide as an example for interested users. Using a vector of real(2) of length 2, in combination with cray pointers, results in very efficient updates of the subMatrix data:
use vector_types
WMMASubMatrix(WMMAMatrixC, 16, 16, 16, Real, WMMAKind2) :: sd
CUFVector(N2, Real, 2), device :: cv, dc(*)
pointer(dp, dc)
CUFReal2 :: xoff
dp = loc(sd%x(1))
xoff = CUFreal(10, kind=2)
cv = makeCUFVector(xoff,xoff)
do klp = 1, maxtimes
if (wmmaAny(sd .gt. xtol)) then
do i = 1, size(sd%x)/2
dc(i) = dc(i) – cv
end do
end if
end do
We also support using the hardware FMA operations for both the CUFReal2 type and the vector of two real(2) types for efficiency. For example:
d = __fma_rn(a, b, c), which is d = a*b+c.
Host-side features for Tensor Core Programming
Host-side real(2) support is limited. Modern X86 processors support real(4) <-> real(2) type conversion using SSE instructions. Our test code takes advantage of that when possible. The cpuid feature to key on is f16c; we have a function in our runtime to test for that. We’ve also written a scalar version of half2float() and float2half(), the latter taking the current CPU rounding mode into account.
We include versions of these two conversion functions which take 1D and 2D arrays for testing purposes. These should no longer be needed once real(2) support is in the compiler, but the code can be used as a guide.
Testing
We divide tests included with PGI 2019 CUDA Fortran package into three directories to correspond to the three matrix sizes currently supported.
m16n16k16:
- wmma1.CUF: Simplest example, multiply two 16×16 real(2) arrays, real(4) result.
- wmma2.CUF: A Submatrix is row major, real(2) result
- wmma3.CUF: A, B Submatrix is row major, real(2) result
- wmma4.CUF: C Submatrix is real(2), D is real(4)
- wmma5.CUF: Store C Submatrix as row major, real(4) result
- wmma6.CUF: Use Submatrix comparison, merge
- wmma7.CUF: Use Submatrix comparison, all
- wmma8.CUF: Use Submatrix comparison, any, v2real2
m32n8k16:
- wmma1.CUF: Simplest example, 32×16 X 16×8 real(2) arrays, real(4) result.
- wmma2.CUF: B Submatrix is row major, real(2) result
- wmma3.CUF: A, B Submatrix is row major, real(4) result
- wmma4.CUF: C Submatrix is real(2), D is real(4)
- wmma5.CUF: Store C Submatrix as row major, real(4) result
- wmma6.CUF: Use Submatrix comparison, merge
- wmma7.CUF: Use Submatrix comparison, all
- wmma8.CUF: Use Submatrix comparison, count, v2real2
m8n32k16:
- wmma1.CUF: Simplest example, 8×16 X 16×32 real(2) arrays, real(4) result.
- wmma2.CUF: A Submatrix is row major, real(2) result
- wmma3.CUF: B Submatrix is row major, real(4) result
- wmma4.CUF: C Submatrix is real(2), D is real(4)
- wmma5.CUF: Store C Submatrix as row major, real(4) result
- wmma6.CUF: Use Submatrix comparison, merge
- wmma7.CUF: Use Submatrix comparison, count
- wmma8.CUF: Use Submatrix comparison, any, v2real2
Summary
PGI will continue to enhance and add features over the course of the year. We welcome your comments and input. Let us know if there are things you would like to see added or changed. Find more information on PGI Fortran on the product page.
Brent Leback
Customer Support and Premier Services Manager, PGI


